- May -akda Jason Gerald [email protected].
- Public 2024-01-15 08:25.
- Huling binago 2025-01-23 12:50.
Ang halaga ng P ay isang pagsukat sa istatistika na makakatulong sa mga siyentista na matukoy kung tama ang kanilang teorya. Ginagamit ang halagang P upang matukoy kung ang mga resulta ng kanilang eksperimento ay nasa loob ng saklaw ng mga halagang normal para sa mga bagay na pinag-aralan. Kadalasan, kung ang halaga ng P ng isang hanay ng data ay nahuhulog sa ibaba ng isang tiyak na natukoy na halaga (halimbawa, 0.05), tatanggihan ng mga siyentista ang null na teorya ng kanilang eksperimento - sa madaling salita, aalisin nila ang isang teorya kung saan ang variable ng pang-eksperimentong walang makabuluhang epekto.sa resulta. Ngayon, ang mga halagang p ay karaniwang matatagpuan sa mga talahanayan ng sanggunian sa pamamagitan ng pagkalkula ng chi square na halaga.
Hakbang

Hakbang 1. Tukuyin ang inaasahang mga resulta ng iyong eksperimento
Karaniwan, kapag ang mga siyentipiko ay nagsasagawa ng isang eksperimento at suriin ang mga resulta, mayroon na silang ideya ng normal o ordinaryong mga resulta muna. Maaari itong batay sa mga resulta ng nakaraang mga eksperimento, maaasahang mga hanay ng data ng pagmamasid, siyentipikong panitikan, at / o iba pang mga mapagkukunan. Para sa iyong eksperimento, tukuyin ang iyong inaasahang resulta at isulat ito bilang isang numero.
Halimbawa: Ipagpalagay na ang isang nakaraang pag-aaral ay ipinakita na, sa pambansang antas, ang mga mabilis na tiket ay naibigay nang mas madalas sa mga pulang kotse kaysa sa mga asul na kotse. Ipagpalagay na ang average na resulta sa pambansang antas ay nagpapakita ng isang ratio ng 2: 1 na may mas maraming ratio ng mga pulang kotse. Nais naming malaman kung ang pulisya sa aming lungsod ay nakakakuha din ng parehong pagkahilig sa pamamagitan ng pag-aaral ng mabilis na tiket na inisyu ng pulisya sa aming lungsod. Kung kumuha kami ng isang random na sample ng 150 mga tiket ng pagbilis na ibinigay sa parehong pula at asul na mga kotse sa aming lungsod, aasahan namin 100 para sa pulang kotse at 50 para sa mga asul na kotse kung ang unit ng pulisya sa aming lungsod ay nagbibigay ng isang tiket alinsunod sa paghahambing sa pambansang antas.

Hakbang 2. Tukuyin ang iyong mga obserbasyong pang-eksperimento
Ngayon na natukoy mo ang iyong inaasahang halaga, maaari mong patakbuhin ang iyong eksperimento at hanapin ang totoong halaga (o pagmamasid). Muli, isulat ang resulta bilang isang numero. Kung manipulahin natin ang ilang mga kundisyong pang-eksperimento at ang naobserbahang mga resulta ay naiiba mula sa inaasahang mga resulta, mayroong dalawang posibilidad: alinman nangyari ito nang hindi sinasadya, o ang pagmamanipula natin ng mga pang-eksperimentong variable na sanhi ng pagkakaiba-iba. Ang layunin ng paghahanap ng p-halaga ay karaniwang upang matukoy kung ang mga naobserbahang resulta ay naiiba mula sa inaasahang mga resulta sa isang punto kung saan ang null na teorya - ang teorya na walang kaugnayan sa pagitan ng pang-eksperimentong variable at ng mga naobserbahang resulta - ay hindi maaaring tanggihan.
Halimbawa: Ipagpalagay, sa aming lungsod, random na pipiliin namin ang 150 mga tiket ng pagbibilis na iginawad sa parehong pula at asul na mga kotse. Nakukuha natin 90 isang tiket para sa isang pulang kotse at 60 para sa asul na kotse. Ito ay naiiba mula sa resulta na inaasahan kong ibig sabihin 100 at 50. Ang aming pang-eksperimentong pagmamanipula ba (sa kasong ito, ang pagbabago ng mapagkukunan ng data mula sa pambansa patungo sa lokal) ay sanhi ng anumang pagbabago sa mga resulta, o ang aming pulisya sa lungsod ay may parehong pagkahilig tulad ng pambansang antas, at napansin lamang namin ang pagkakataon? Tutulungan kami ng halaga ng p na matukoy ito.

Hakbang 3. Tukuyin ang mga degree ng kalayaan para sa iyong eksperimento
Ang mga antas ng kalayaan ay isang sukatan ng dami ng pagkakaiba-iba sa pag-aaral, na tinutukoy ng bilang ng mga kategorya na iyong sinusuri. Ang equation para sa antas ng kalayaan ay Mga antas ng kalayaan = n-1, kung saan n ang bilang ng mga kategorya o variable na nasuri sa iyong eksperimento.
-
Halimbawa: Ang aming eksperimento ay may dalawang kategorya ng mga resulta: isa para sa pulang kotse at isa para sa asul na kotse. Sa gayon, sa aming eksperimento, mayroon kaming 2-1 = 1 antas ng kalayaan.
Kung ihinahambing namin ang pula, asul, at berde na mga kotse, magkakaroon tayo
Hakbang 2. antas ng kalayaan at iba pa.

Hakbang 4. Paghambingin ang inaasahang mga resulta sa napansin na mga resulta gamit ang chi square
Chi parisukat (nakasulat x2) ay isang numerong halaga na sumusukat sa pagkakaiba sa pagitan ng inaasahan at sinusunod na mga halaga mula sa eksperimento. Ang equation para sa chi squared ay: x2 = ((o-e)2/ e), kung saan o ang naobserbahang halaga at e ang inaasahang halaga. Idagdag ang mga resulta ng equation na ito para sa lahat ng posibleng mga kinalabasan (tingnan sa ibaba).
- Tandaan na ang equation na ito ay gumagamit ng (sigma) operator. Sa madaling salita, kailangan mong kalkulahin ((| o-e | -.05)2/ e) para sa bawat posibleng kinalabasan, pagkatapos ay idagdag ang mga resulta upang makuha ang chi square na halaga. Sa aming halimbawa, mayroon kaming dalawang mga resulta - isang kotse na nakakakuha ng pula o isang asul na tiket. Kaya, maaari nating kalkulahin ((o-e)2/ e) dalawang beses - isang beses para sa pulang kotse at isang beses para sa asul na kotse.
-
Halimbawa: I-plug natin ang ating mga inaasahang halaga at obserbasyon sa equation x2 = ((o-e)2/ e). Tandaan na, dahil sa operator ng sigma, kailangan nating mag-compute ((o-e)2/ e) dalawang beses - isang beses para sa pulang kotse at isang beses para sa asul na kotse. Ang mga hakbang sa pagproseso ay ang mga sumusunod:
- x2 = ((90-100)2/100) + (60-50)2/50)
- x2 = ((-10)2/100) + (10)2/50)
- x2 = (100/100) + (100/50) = 1 + 2 = 3.

Hakbang 5. Pumili ng isang antas ng kabuluhan
Ngayong alam na natin ang degree ng kalayaan ng aming pang-eksperimentong at ang chi square na halaga, mayroon lamang isang huling bagay na kailangan nating gawin bago makita ang aming p-halaga - kailangan nating matukoy ang antas ng kabuluhan. Karaniwan, ang antas ng kahalagahan ay isang pagsukat kung gaano tayo sigurado sa aming mga resulta - isang mababang antas ng kahalagahan ay tumutugma sa isang mababang posibilidad na ang kinalabasan ng isang eksperimento ay dahil sa pagkakataon at kabaligtaran. Ang antas ng kahalagahan ay nakasulat bilang isang decimal (hal. 0.01), na tumutugma sa porsyento ng posibilidad na ang kinalabasan ng eksperimento ay dahil sa pagkakataon (sa kasong ito, 1%).
- Sa pamamagitan ng kombensiyon, ang mga siyentipiko ay karaniwang nagtatakda ng isang halaga ng kahalagahan para sa kanilang mga eksperimento sa 0.05 o 5 porsyento. Nangangahulugan ito na ang mga pang-eksperimentong resulta na tumutugma sa antas ng kahalagahan na ito ay mayroong 5% na pagkakataon na magkataon. Sa madaling salita, mayroong isang 95% na pagkakataon na ang mga resulta ay dahil sa pagmamanipula ng syentista ng mga pang-eksperimentong variable, at hindi pagkakataon. Para sa karamihan ng mga eksperimento, 95% kumpiyansa tungkol sa ugnayan sa pagitan ng dalawang variable, ay itinuturing na matagumpay sa pagpapakita ng ugnayan sa pagitan ng dalawa.
- Halimbawa: Para sa aming halimbawa ng pula at asul na kotse, sundin natin ang kasunduang pang-agham at tukuyin ang antas ng kahalagahan ng 0, 05.
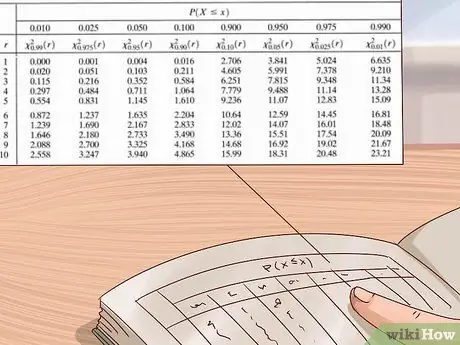
Hakbang 6. Gamitin ang talahanayan ng pamamahagi ng chi square upang tantyahin ang iyong p-halaga
Ang mga siyentista at istatistika ay gumagamit ng malalaking talahanayan ng mga halaga upang makalkula ang mga halagang p para sa kanilang mga eksperimento. Ang talahanayan na ito ay karaniwang nakasulat na may patayong axis sa kaliwa na ipinapakita ang mga degree ng kalayaan at ang pahalang na axis sa tuktok na nagpapakita ng mga p-halaga. Gamitin ang talahanayan na ito sa pamamagitan ng unang paghahanap ng iyong mga degree ng kalayaan, pagkatapos ay basahin ang mga hilera mula kaliwa hanggang kanan hanggang sa makita mo ang unang halaga na mas malaki kaysa sa iyong chi square na halaga. Tingnan ang p-halaga sa tuktok ng haligi - ang iyong p-halaga ay nasa pagitan ng halagang ito at ang susunod na pinakamalaking halaga (ang kanang halaga ay sa kaliwa nito).
- Ang mga talahanayan ng pamamahagi ng Chi square ay magagamit mula sa iba't ibang mga mapagkukunan - madali silang matagpuan sa online o sa mga aklat na pang-agham o istatistika. Kung wala ka, gamitin ang talahanayan na ipinakita sa larawan sa itaas o isang libreng online na talahanayan, tulad ng ibinigay ng medcalc.org dito.
-
Halimbawa: Ang aming chi square ay 3. Kaya't gamitin natin ang talahanayan ng pamamahagi ng chi square sa larawan sa itaas upang makahanap ng isang tinatayang p-halaga. Dahil alam namin na mayroon lamang ang aming eksperimento
Hakbang 1. degree ng kalayaan, magsisimula tayo mula sa tuktok na talahanayan. Pumunta kami mula kaliwa hanggang kanan sa hilera na ito hanggang sa makahanap kami ng halagang mas mataas kaysa sa
Hakbang 3. - ang aming chi square na halaga. Ang unang halagang nahanap namin ay 3.84. Sa pagtingin sa kolum na ito, nakikita namin na ang katumbas na p-halaga ay 0.05. Nangangahulugan ito na ang aming p-halaga ay sa pagitan ng 0.05 at 0.1 (Susunod na pinakamalaking p-halaga sa talahanayan).

Hakbang 7. Magpasya kung tatanggihan o ipagtanggol ang iyong null na teorya
Dahil natagpuan mo ang isang tinatayang p-halaga para sa iyong eksperimento, maaari kang magpasya kung tatanggihan o hindi ang null na teorya ng iyong eksperimento (bilang paalala, ito ang teorya na ang variable na pang-eksperimento na iyong minamanipula ay walang epekto sa mga resulta na napansin mo). Kung ang iyong p-halaga ay mas mababa kaysa sa iyong halaga ng kahalagahan, binabati kita - napatunayan mo na mayroong isang mataas na posibilidad na mayroong isang ugnayan sa pagitan ng mga variable na iyong minamanipula at iyong mga obserbasyon. Kung ang iyong p-halaga ay mas malaki kaysa sa iyong halaga ng kahalagahan, hindi mo masasabi na may katiyakan na ang mga resulta na iyong sinusunod ay resulta ng simpleng pagkakataon o pagmamanipula lamang ng iyong eksperimento.
- Halimbawa: Ang aming p-halaga ay nasa pagitan ng 0.05 at 0.1. Iyon ay, hindi ito nangangahulugang mas mababa sa 0.05, kaya, sa kasamaang palad, tayo hindi maitatanggi ang aming null na teorya. Nangangahulugan ito na hindi namin maaabot ang minimum na 95% na limitasyon sa kumpiyansa na itinakda namin upang masabing ang pulisya sa aming lungsod ay nagbibigay ng mga tiket sa tiket sa mga pula at asul na mga kotse sa isang ratio na medyo naiiba mula sa pambansang average.
- Sa madaling salita, mayroong 5-10% na pagkakataon na ang aming mga obserbasyon ay hindi resulta ng isang pagbabago sa lokasyon (pinag-aaralan ang aming lungsod, at hindi ang buong bahagi), ngunit nagkataon lamang. Dahil naghahanap kami ng posibilidad na mas mababa sa 5%, hindi namin masasabi na kami nakumbinsi na ang pulisya sa ating lungsod ay may posibilidad na mag-ticket ng mga pulang kotse - mayroong isang bahagyang ngunit ayon sa istatistika ibang-iba ang posibilidad na wala silang ugaliing ito.
Mga Tip
- Ang isang siyentipikong calculator ay gagawing mas madali ang mga kalkulasyon. Maaari ka ring maghanap para sa mga calculator sa online.
- Maaari mong kalkulahin ang mga p-halaga gamit ang maraming mga programa sa computer, kabilang ang karaniwang ginagamit na software ng spreadsheet at mas dalubhasang statistic software.






