Ang isang rhombus ay isang quadrilateral na may apat na pantay na panig. Mayroong tatlong mga formula para sa paghahanap ng lugar ng isang rhombus. Sundin lamang ang mga hakbang na ito upang malaman kung paano.
Hakbang
Paraan 1 ng 3: Paggamit ng dayagonal
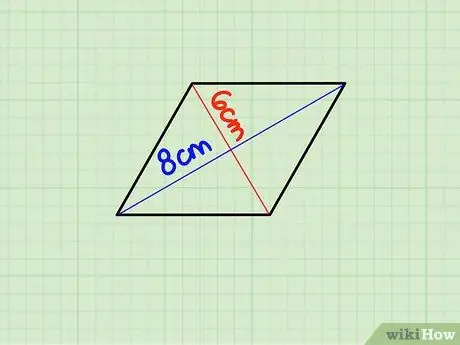
Hakbang 1. Hanapin ang haba ng bawat dayagonal
Ang mga diagonal ng isang rhombus ay mga linya na kumokonekta sa tapat ng mga vertex (sulok) sa gitna ng hugis. Ang mga diagonal ng isang rhombus ay patayo at bumubuo ng apat na kanang triangles sa pamamagitan ng punto ng intersection.
Sabihin nating ang dayagonal ay 6 cm at ang haba ay 8 cm
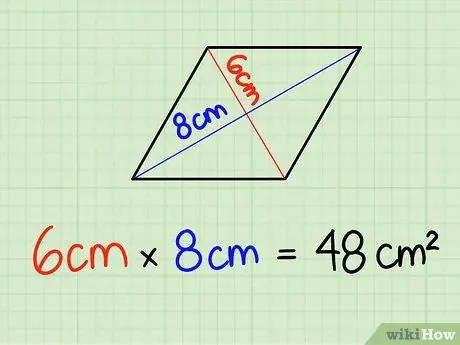
Hakbang 2. I-multiply ang haba ng dayagonal
Isulat lamang ang haba ng dayagonal at magparami. Sa kasong ito, 6 cm x 8 cm = 48 cm2. Huwag kalimutang i-multiply ang mga unit dahil nagtatrabaho kami sa mga square unit.
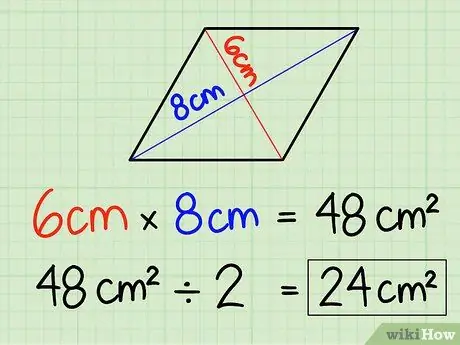
Hakbang 3. Hatiin ang resulta sa 2
Dahil 6 cm x 8 cm = 48 cm2, hatiin lamang ang resulta sa pamamagitan ng 2.48 cm2/ 2 = 24 cm2. Ang lugar ng isang rhombus ay 24 cm2.
Paraan 2 ng 3: Paggamit ng Batayan at Taas
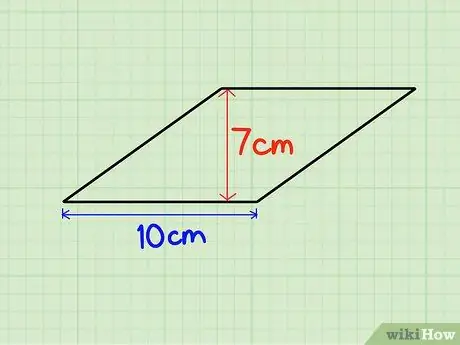
Hakbang 1. Hanapin ang base at taas
Maaari din nating paramihin ang taas ng rhombus sa haba ng gilid ng rhombus. Sabihin nating ang taas ng rhombus ay 7 cm at ang base ay 10 cm.
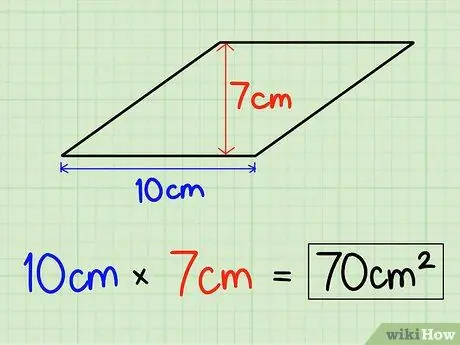
Hakbang 2. I-multiply ang base at ang taas
Matapos malaman ang base at taas ng rhombus, hanapin ang lugar ng hugis sa pamamagitan ng pagpaparami nito. Kaya, 10 cm x 7 cm = 70 cm2. Ang lugar ng isang rhombus ay 70 cm2.
Paraan 3 ng 3: Paggamit ng Trigonometry
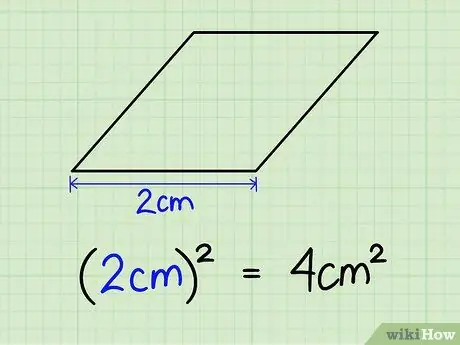
Hakbang 1. Itama ang haba ng anumang panig
Ang isang rhombus ay may apat na pantay na panig, kaya't hindi mahalaga kung aling panig ang pipiliin namin. Sabihin nating ang panig ay may haba na 2 cm. 2cm x 2cm = 4cm2.
Hakbang 2. Pag-multiply sa sine ng isang sulok
Hindi alintana kung aling anggulo ang pipiliin natin. Sabihin nating ang isa sa mga anggulo ay 33 degree. Paramihin lang ang sine (33) ng 4 cm2 upang makuha ang lugar ng rhombus. (2cm)2 x sine (33) = 4 cm2 x 1 = 4 cm2. Ang lugar ng isang rhombus ay 4 cm2.
