- May -akda Jason Gerald [email protected].
- Public 2024-01-19 22:14.
- Huling binago 2025-01-23 12:50.
Mahirap ang matematika. Madaling kalimutan kahit na ang mga pangunahing konsepto kapag sinubukan mong tandaan ang maraming iba't ibang mga prinsipyo at pamamaraan. Narito ang dalawang sariwang paraan upang gawing simple ang mga praksyon.
Hakbang
Paraan 1 ng 4: Paggamit ng Pinakadakilang Karaniwang Kadahilanan

Hakbang 1. Isulat ang mga kadahilanan ng numerator at denominator
Ang mga kadahilanan ay mga numero na maaari mong i-multiply upang makakuha ng isa pang numero. Halimbawa, ang 3 at 4 ay mga kadahilanan ng 12 sapagkat maaari mong i-multiply ang mga ito upang makakuha ng 12. Upang isulat ang mga kadahilanan ng isang numero, kailangan mo lamang isulat ang lahat ng mga numero na maaaring i-multiply upang makuha ang numerong iyon, at nahahati sa pamamagitan ng mga kadahilanan.
-
Isulat ang mga kadahilanan ng numero mula sa pinakamaliit hanggang sa pinakamalaki, nang hindi nalilimutan na isama ang salik 1. Halimbawa, narito kung paano mo isusulat ang numerator at denominator ng maliit na bahagi ng 24/32:
- 24: 1, 2, 3, 4, 6, 8, 12, 24.
- 32: 1, 2, 4, 8, 16, 32.

Hakbang 2. Hanapin ang pinakadakilang karaniwang kadahilanan (GCF) ng numerator at denominator
Ang GCF ay ang pinakamalaking bilang na maaaring pantay na maghati ng dalawa o higit pang mga numero. Matapos mong isulat ang lahat ng mga kadahilanan ng numero, ang kailangan mo lang gawin ay hanapin ang pinakamalaking bilang na pareho sa parehong listahan ng mga kadahilanan.
-
24: 1, 2, 3, 4, 6,
Hakbang 8., 12, 24.
-
32: 1, 2, 4,
Hakbang 8., 16, 32.
-
Ang GCF ng 24 at 32 ay 8 dahil ang 8 ang pinakamalaking bilang na maaaring pantay na hatiin ang 24 at 32.

Hakbang 3. Hatiin ang numerator at maliit na bahagi ng GCF
Ngayon na nakuha mo ang GCF, ang kailangan mo lang gawin ay hatiin ang numerator at denominator ng numerong iyon upang gawing simple ang iyong maliit na bahagi sa pinakasimpleng form nito. Narito kung paano ito gawin:
- 24/8 = 3
- 32/8 = 4
- Ang simpleng praksyon ay 3/4.

Hakbang 4. Suriin ang iyong trabaho
Kung nais mong tiyakin na napasimple mo ang maliit na bahagi, kailangan mo lamang i-multiply ang bagong numerator at denominator ng kanilang GCF upang maibalik ang orihinal na praksyon. Narito kung paano ito gawin:
- 3 * 8 = 24
- 4 * 8 = 32
-
Bumalik ka sa orihinal na form, na kung saan ay 24/32.
Maaari mo ring suriin ang maliit na bahagi upang matiyak na hindi ito mas madali pa. Yamang ang 3 ay isang pangunahing numero, maaari lamang itong paghatiin ng 1 at ng kanyang sarili, at ang apat ay hindi mahahati ng 3, kaya't ang maliit na bahagi ay hindi maaaring gawing mas simple
Paraan 2 ng 4: Panatilihin ang Paghahati ng Maliliit na Mga Numero

Hakbang 1. Pumili ng isang maliit na numero
Gamit ang pamamaraang ito, pumili ka lamang ng isang maliit na numero, tulad ng 2, 3, 4, 5 o 7, upang magsimula ka. Tingnan ang mga praksyon upang matiyak na ang bawat bahagi ay mahahati sa pamamagitan ng bilang na iyong pinili. Halimbawa, kung mayroon kang isang maliit na bahagi 24/108, huwag pumili ng 5 dahil hindi sila mahahati sa 5. Gayunpaman, kung mayroon kang isang maliit na bahagi ng 25/60, 5 ang tamang numero na gagamitin.
Para sa maliit na bahagi ng 24/32, 2 ay isang mahusay na numero. Dahil ang parehong mga numero ay kahit na mga numero, ang mga ito ay nahahati sa pamamagitan ng 2

Hakbang 2. Hatiin ang numerator at denominator ng maliit na bahagi ng bilang
Ang bagong maliit na bahagi ay binubuo ng isang bagong numerator at denominator, na nakukuha mo pagkatapos hatiin ang tuktok at ibaba ng maliit na bahagi ng 24/32 ng 2. Narito kung paano ito gawin:
- 24/2 = 12
- 32/2 = 16
- Ang iyong bagong maliit na bahagi ay 12/16.
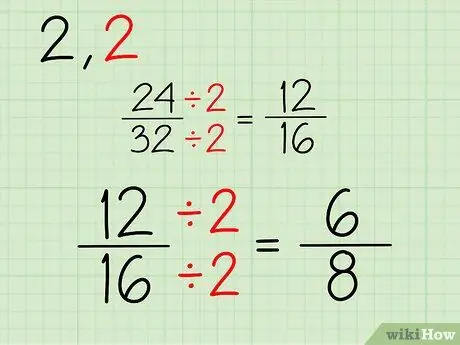
Hakbang 3. Ulitin
Ipagpatuloy ang prosesong ito. Dahil ang parehong mga numero ay kahit na mga numero, maaari mong panatilihin ang paghahati ng 2. Kung ang isa o pareho ng mga numerator at denominator ay mga kakaibang numero, maaari mong subukang hatiin ang isa pang numero. Narito ang proseso para sa pagpapadali ng 12/16 maliit na bahagi:
- 12/2 = 6
- 16/2 = 8
- Ang iyong bagong maliit na bahagi ay 6/8.

Hakbang 4. Patuloy na hatiin ang numero hanggang sa hindi na ito mahati
Ang bagong numerator at denominator ay kahit na mga numero, sa gayon maaari mong panatilihin ang paghahati ng 2. Narito kung paano ito gawin:
- 6/2 = 3
- 8/2 = 4
- Ang iyong bagong maliit na bahagi ay 3/4.

Hakbang 5. Siguraduhin na ang maliit na bahagi ay hindi maaaring gawing mas simple
Sa maliit na bahagi 3/4, ang 3 ay isang pangunahing numero, kaya't ang mga salik ay 1 at mismo, at ang 4 ay hindi mahahati ng 3, kaya't ang praksiyon ay hindi maaaring gawing mas simple. Kung ang numerator o denominator ng maliit na bahagi ay hindi na mahahati sa bilang na iyong napili, maaari mo pa rin itong hatiin sa ibang numero.
Halimbawa, kung mayroon kang maliit na bahagi ng 10/40, at hinati mo ang numerator at denominator ng 5, ang resulta ay 2/8. Hindi mo maaaring panatilihin ang paghahati ng numerator at maliit na bahagi ng 5, ngunit maaari mong hatiin ang pareho sa 2 kaya ang resulta ay 1/4

Hakbang 6. Suriin ang iyong trabaho
I-multiply ang 3/4 ng 2/2 muli ng tatlong beses, upang matiyak na makukuha mo ang paunang praksyon, na 24/32. Narito kung paano ito gawin:
- 3/4 * 2/2 = 6/8
- 6/8 * 2/2 = 12/16
- 12/16 * 2/2 = 24/32.
- Pansinin na hinahati mo ang 24/32 ng 2 * 2 * 2, na kapareho ng paghahati ng 8, ang pinakamalaking GCF na 24 at 32.
Paraan 3 ng 4: Pagsulat ng Mga Kadahilanan

Hakbang 1. Isulat ang iyong maliit na bahagi
Mag-iwan ng isang malaking puwang sa kanang bahagi ng iyong papel - kakailanganin mo ito upang isulat ang mga kadahilanan.

Hakbang 2. Isulat ang mga salik ng numerator at denominator
Nag-iisa ang mga kadahilanan ng dalawa. Ang pinakamadaling paraan ay para sa mga salik na naisulat sa tuktok ng bawat isa. Magsimula sa bilang 1 at isulat ang mga kadahilanan.
-
Halimbawa, kung ang iyong maliit na bahagi ay 24/60, magsimula sa 24.
Isulat: 24 - 1, 2, 3, 4, 6, 8, 12, 24
-
Pagkatapos, ang bilang 60.
Isulat: 60 - 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60

Hakbang 3. Hanapin at hatiin ang pinakadakilang kadahilanan
Ang term na ito ay maaaring nakasulat bilang GCF sa iyong naka-print na libro. Ano ang pinakamalaking bilang na maaaring hatiin ang numerator at denominator? Anuman ang numero, hatiin ang parehong mga numero sa numerong iyon.
Para sa aming halimbawa, ang pinakamalaking bilang na isang kadahilanan ng parehong mga numero ay 12. Sa gayon, hinati namin ang 24 ng 12 at 60 ng 12, na binibigyan kami ng 2/5 - ang aming simpleng bahagi
Paraan 4 ng 4: Paggamit ng Punong Punong Punong

Hakbang 1. Hanapin ang pangunahing mga kadahilanan ng numerator at denominator
Ang isang pangunahing numero ay isang numero na hindi maaaring hatiin ng anumang iba pang mga numero (maliban sa kanyang sarili at 1, siyempre). Ang 2, 3, 5, 7, at 11 ay mga halimbawa ng pangunahing numero.
- Magsimula sa numerator. Mula sa 24, nahati sa 2 at 12. Dahil ang prime ay isa nang pangunahing numero, hindi mo na kailangang hatiin pa ito! Pagkatapos break 12 sa 2 numero: 2 at 6. 2 ay pangunahing numero - mahusay! Hatiin ngayon ang 6 sa 2 mga numero: 2 at 3. Mayroon ka na ngayong 2, 2, 2 at 3 bilang iyong pangunahing mga numero.
- Ngayon magtrabaho sa denominator. Mula sa 60, hatiin ang iyong puno sa 2 at 30. 30 pagkatapos hatiin sa 2 at 15. Pagkatapos hatiin ang 15 sa 3 at 5, na kapwa mga punong numero. Ngayon mayroon kang 2, 2, 3, at 5 bilang iyong pangunahing mga numero.
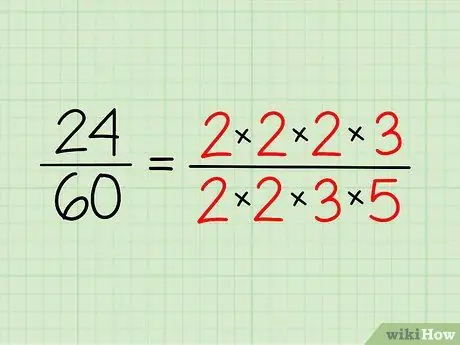
Hakbang 2. Isulat ang pangunahing factorization ng bawat numero
Isulat ang pangunahing mga numero na mayroon ka para sa bawat numero at isulat ang mga ito sa form na pagpaparami. Hindi mo kailangang i-multiply ito - paraan lamang ito upang mas madaling makita ito.
- Kaya, para sa 24, mayroon kang 2 x 2 x 2 x 3 = 24.
- Para sa 60, mayroon kang 2 x 2 x 3 x 5 = 60

Hakbang 3. Tanggalin ang parehong mga kadahilanan
Ang anumang numero na bahagi ng parehong mga numero ay maaaring itapon. Sa halimbawang ito, ang pantay na mga kadahilanan ay isang pares ng 2s at isa 3. Paalam!
- Ang natitira ay 2 at 5 - o 2/5! Ang parehong sagot na nakuha namin sa itaas.
- Kung ang numerator at denominator ng maliit na bahagi ay pantay na mga numero, huwag lamang hatiin sa dalawa. Magpatuloy na gawin ang paghahati hanggang sa ang numero na makuha mo ay hindi maaaring hatiin muli.






